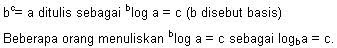Logaritma adalah operasi matematika yang merupakan kebalikan dari eksponen atau pemangkatan.
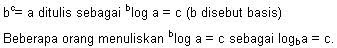
Mencari nilai logaritma:
Cara untuk mencari nilai logaritma antara lain dengan menggunakan:
* Tabel
* Kalkulator (yang sudah dilengkapi fitur log)
Kegunaan logaritma:
Logaritma
sering digunakan untuk memecahkan persamaan yang pangkatnya tidak
diketahui. Turunannya mudah dicari dan karena itu logaritma sering
digunakan sebagai solusi dari integral. Dalam persamaan bn = x, b dapat
dicari dengan pengakaran, n dengan logaritma, dan x dengan fungsi
eksponensial.
Rumus logaritma;

Sains dan teknik:
Dalam
sains, terdapat banyak besaran yang umumnya diekspresikan dengan
logaritma. Sebabnya, dan contoh-contoh yang lebih lengkap, dapat dilihat
di skala logaritmik.
* Negatif dari logaritma berbasis 10
digunakan dalam kimia untuk mengekspresikan konsentrasi ion hidronium
(pH). Contohnya, konsentrasi ion hidronium pada air adalah 10−7 pada
suhu 25 °C, sehingga pH-nya 7.
* Satuan bel (dengan simbol B)
adalah satuan pengukur perbandingan (rasio), seperti perbandingan nilai
daya dan tegangan. Kebanyakan digunakan dalam bidang telekomunikasi,
elektronik, dan akustik. Salah satu sebab digunakannya logaritma adalah
karena telinga manusia mempersepsikan suara yang terdengar secara
logaritmik. Satuan Bel dinamakan untuk mengenang jasa Alexander Graham
Bell, seorang penemu di bidang telekomunikasi. Satuan desibel (dB), yang
sama dengan 0.1 bel, lebih sering digunakan.
* Skala Richter mengukur intensitas gempa bumi dengan menggunakan skala logaritma berbasis 10.
* Dalam astronomi, magnitudo yang mengukur terangnya bintang
menggunakan skala logaritmik, karena mata manusia mempersepsikan terang
secara logaritmik.
Penghitungan yang lebih mudah:
Logaritma
memindahkan fokus penghitungan dari bilangan normal ke pangkat-pangkat
(eksponen). Bila basis logaritmanya sama, maka beberapa jenis
penghitungan menjadi lebih mudah menggunakan logaritma:
Rumus dasar logaritma;

Sifat-sifat
diatas membuat penghitungan dengan eksponen menjadi lebih mudah, dan
penggunaan logaritma sangat penting, terutama sebelum tersedianya
kalkulator sebagai hasil perkembangan teknologi modern.
Untuk
mengkali dua angka, yang diperlukan adalah melihat logaritma
masing-masing angka dalam tabel, menjumlahkannya, dan melihat antilog
jumlah tersebut dalam tabel. Untuk mengitung pangkat atau akar dari
sebuah bilangan, logaritma bilangan tersebut dapat dilihat di tabel,
lalu hanya mengkali atau membagi dengan radix pangkat atau akar
tersebut.
Bilangan Berpangkat Dan Bentuk Akar
Bilangan Bulat dengan Eksponen Bilangan Bulat Positif
Masih ingat bentuk berikut :
3
2 = 3 x 3
2
3 = 2 x 2 x 2
5
6 = 5 x 5 x 5 x 5 x 5 x 5
Demikian seterusnya sehingga diperoleh bentuk umum sebagai berikut.

Dengan a bilangan bulat dan n bilangan bulat positif Dari pengertian di atas akan diperoleh sifat-sifat berikut.
Sifat 1
an x an = am + n
2
4 x 2
3 = (2 x 2 x 2 x 2 )x(2 x 2 x 2 )
= 2 x 2 x 2 x 2 x 2 x 2 x 2
= 27
= 2
4+3
Sifat 2
am : an = am - n, m > n
5
5 : 5
3 = (5 x 5 x 5 x 5 x 5) : (5 x 5 x 5)
= 5 x 5
= 52
= 5
5 - 3
Sifat 3
(am)n = am x n
(3
4)
2 = 3
4 x 3
4
= (3 x 3 x 3 x 3) x (3 x 3 x 3 x 3)
= (3 x 3 x 3 x 3 x 3 x 3 x 3 x 3)
= 38
= 3
4 x 2
Sifat 4
(a x b)m = am x bm
(4 x 2)
3 = (4 x 2) x (4 x 2) x (4 x 2)
= (4 x 4 x 4) x (2 x 2 x 2)
= 4
3 x 2
3
Sifat 5
(a : b)m = am : bm
(6 : 3)
4 = (6 : 3) x (6 : 3) x (6 : 3) x (6 : 3)
= (6 x 6 x 6 x 6) : (3 x 3 x 3 x 3)
= 6
4 : 3
4
Bilangan Bulat dengan Eksponen Bilangan Bulat Negatif

Dari pola bilangan itu dapat disimpulkan bahwa 2
0 = 1 dan 2
-n =
1/
2n , secara umum dapat ditulis :

Pecahan Berpangkat Bilangan Bulat
Kita telah mengetahui bahwa
pecahan adalah bilangan dalam bentuk dengun a dan b bilangan bulat (b ≠
0). Bagaimanakah jika pecahan dipangkatkan dengan bilangan bulat? Untuk
menentukan hasil pecahan yang dipangkatkan dengan bilangan bulat,
caranya sama dengan menentukan hasil bilangan bulat yang dipangkatkan
dengan bilangan bulat.
Contoh:
Tentukan hasil berikut ini!
(
1/
2)
5
Jawab :

Bentuk Akar dan Bilangan Berpangkat Pecahan
Bilangan Rasional dan Irasional
Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk
a/
b
dengan a, b bilangan bulat dan b ≠ 0. Bilangan rasional merupakan
gabungan dari bilangan bulat, nol, dan pecahan. Contoh bilangan rasional
adalah -5,
-1/
2, 0, 3,
3/
4, dan
5/
9.
Sebaliknya,
bilangan irasional adalah bilangan yang tidak dapat dinyatakan dalam bentuk
a/
b dengan a, b bilangan bulat dan b ≠ 0.
Contoh
bilangan irasional adalah . Bilangan-bilangan tersebut, jika dihitung
dengan kalkulator merupakan desimal yang tak berhenti atau bukan desimal
yang berulang. Misalnya
√2 = 1,414213562 .... Selanjutnya, gabungan anrara bilangan rasional dan irasional disebut bilangan real.
Bentuk Akar
Berdasarkan pembahasan sebelumnya, contoh bilangan irasional
adalah √2 dan √5 . Bentuk seperti itu disebut bentuk akar. Dapatkah
kalian menyebutkan contoh yang lain?
Bentuk akar adalah akar dari suatu bilangan yang hasilnya bukan bilangan Rasional.
Bentuk akar dapat disederhanakan menjadi perkalian dua buah akar pangkat bilangan dengan salah satu akar memenuhi definisi
√a
2 = a jika a ≥ 0, dan –a jika a < 0
Contoh :
Sederhanakan bentuk akar berikut √75
Jawab :
√75 = √25x3 = √25 x √3 = 5√3
Mengubah Bentuk Akar Menjadi Bilangan Berpangkat Pecahan dan Sebaliknya
Bentuk √a dengan a bilangan bulat tidak negatif disebut bentuk akar
kuadrat dengan syarat tidak ada bilangan yang hasil kuadratnya sama
dengan a. oleh karena itu √2,√3, √5, √10, √15 dan √19 merupakan bentuk
akar kuadrat. Untuk selanjutnya, bentuk akar
n√a
m dapat ditulis a
m/n (dibaca: a pangkat m per n). Bentuk a
m/n disebut bentuk pangkat pecahan.
contoh :
 jawab :
jawab :

Operasi Aljabar pada Bentuk Akar
Penjumlahan dan Pengurangan
Penjumlahan dan pengurangan pada bentuk akar dapat dilakukan jika memiliki suku-suku yang sejenis.

kesimpulan :
jika a, c = Rasional dan b ≥ 0, maka berlaku
a√b + c√b = (a + c)√b
a√b - c√b = (a - c)√b
Perkalian dan Pembagian
Contoh :
Tentukan hasil operasi berikut :
 jawab :
jawab :

Perpangkatan
Kalian tentu masih ingat bahwa (a^)" = a^'. Rumus tersebut juga berlaku pada operasi perpangkatan dari akar suatu bilangan.
Contoh:

Operasi Campuran
Dengan memanfaatkan sifat-sifat pada bilangan berpangkat, kalian akan
lebih mudah menyelesaikan soal-soal operasi campuran pada bentuk
akarnya. Sebelum melakukan operasi campuran, pahami urutan operasi
hitung berikut.
- Prioritas yang didahulukan pada operasi bilangan adalah bilangan-bilangan yang ada dalam tanda kurung.
- Jika tidak ada tanda kurungnya maka
- pangkat dan akar sama kuat;
- kali dan bagi sama kuat;
- tambah dan kurang sama kuat, artinya mana yang lebih awal dikerjakan terlebih dahulu;
- kali dan bagi lebih kuat daripada tambah dan kurang, artinya kali dan bagi dikerjakan terlebih dahulu.
Contoh :

Merasionalkan Penyebut
Dalam perhitungan matematika, sering kita temukan pecahan dengan penyebut bentuk akar, misalnya

Agar nilai pecahan tersebut lebih sederhana maka penyebutnya
harus dirasionalkan terlebih dahulu. Artinya tidak ada bentuk akar pada
penyebut suatu pecahan. Penyebut dari pecahan-pecahan yang akan
dirasionalkan berturut-turut adalah

Merasionalkan penyebut adalah mengubah pecahan dengan penyebut
bilangan irasional menjadi pecahan dengan penyebut bilangan rasional.
Penyebut Berbentuk √b
Jika a dan b adalah bilangan rasional, serta √b adalah bentuk akar maka pecahan
a/
√b dapat dirasionalkan penyebutnya dengan cara mengalikan pecahan tersebut dengan
√b/
√b .
 Contoh :
Contoh :
Sederhanakan pecahan berikut dengan merasionalkan penyebutnya!
 jawab :
jawab :

Penyebut Berbentuk (a+√b) atau (a+√b)
Jika pecahan-pecahan mempunyai penyebut berbentuk (a+√b) atau (a+√b)
maka pecahan tersebut dapat dirasionalkan dengan cara mengalikan
pembilang dan penyebutnya dengan sekawannya. Sekawan dari (a+√b) adalah
(a+√b) adalah dan sebaliknya.
Bukti
 Contoh :
Contoh :
Rasionalkan penyebut pecahan berikut.
 jawab :
jawab :

Penyebut Berbentuk (√b+√d) atau (√b+√d)
Pecahan tersebut dapat dirasionalkan dengan mengalikan pembilang dan
penyebutnya dengan bentuk akar sekawannya, yaitu sebagai berikut.
 Contoh:
Contoh:
Selesaikan soal berikut!
 Jawab :
Jawab :